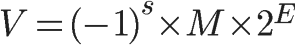计算机指令
计算机指令的简单理解
从软件的角度上来说,CPU是一个执行各种计算指令的逻辑机器。这里的计算指令,好比CPU能听懂的语言,我们把他叫做机器语言(Machine Language)。
不同CPU能听懂的语言不通。例如Intel的CPU和苹果的ARM的CPU,两者能听懂的语言就不太一样。类似这两种CPU支持的语言,就是两组不通的计算机指令集(Instruciton Set)。
一个计算机程序,不可能只有一条指令,而是由成千上万条指令组成的。 但是CPU里不能一直放着所有的指令,因此计算机程序平时都是存储在存储器上的。种程序指令存储在存储器里面的计算机,我们就叫作存储程序型计算机(Stored-program Computer)。
除了 C 这样的编译型的语言之外,不管是 Python 这样的解释型语言,还是 Java 这样使用虚拟机的语言,其实最终都是由不同形式的程序,把我们写好的代码,转换成 CPU 能够理解的机器码来执行的。
只是解释型语言,是通过解释器在程序运行的时候逐句翻译,而 Java 这样使用虚拟机的语言,则是由虚拟机对编译出来的中间代码进行解释,或者即时编译成为机器码来最终执行。
CPU如何运行指令
在 CPU 在软件层面已经为我们做好了封装。对于我们这些做软件的程序员来说,我们只要知道,写好的代码变成了指令之后,是一条一条顺序执行的就可以了。
逻辑上,我们可以认为,CPU 其实就是由一堆寄存器组成的。而寄存器就是 CPU 内部,由多个触发器(Flip-Flop)或者锁存器(Latches)组成的简单电路。触发器和锁存器,其实就是两种不同原理的数字电路组成的逻辑门。
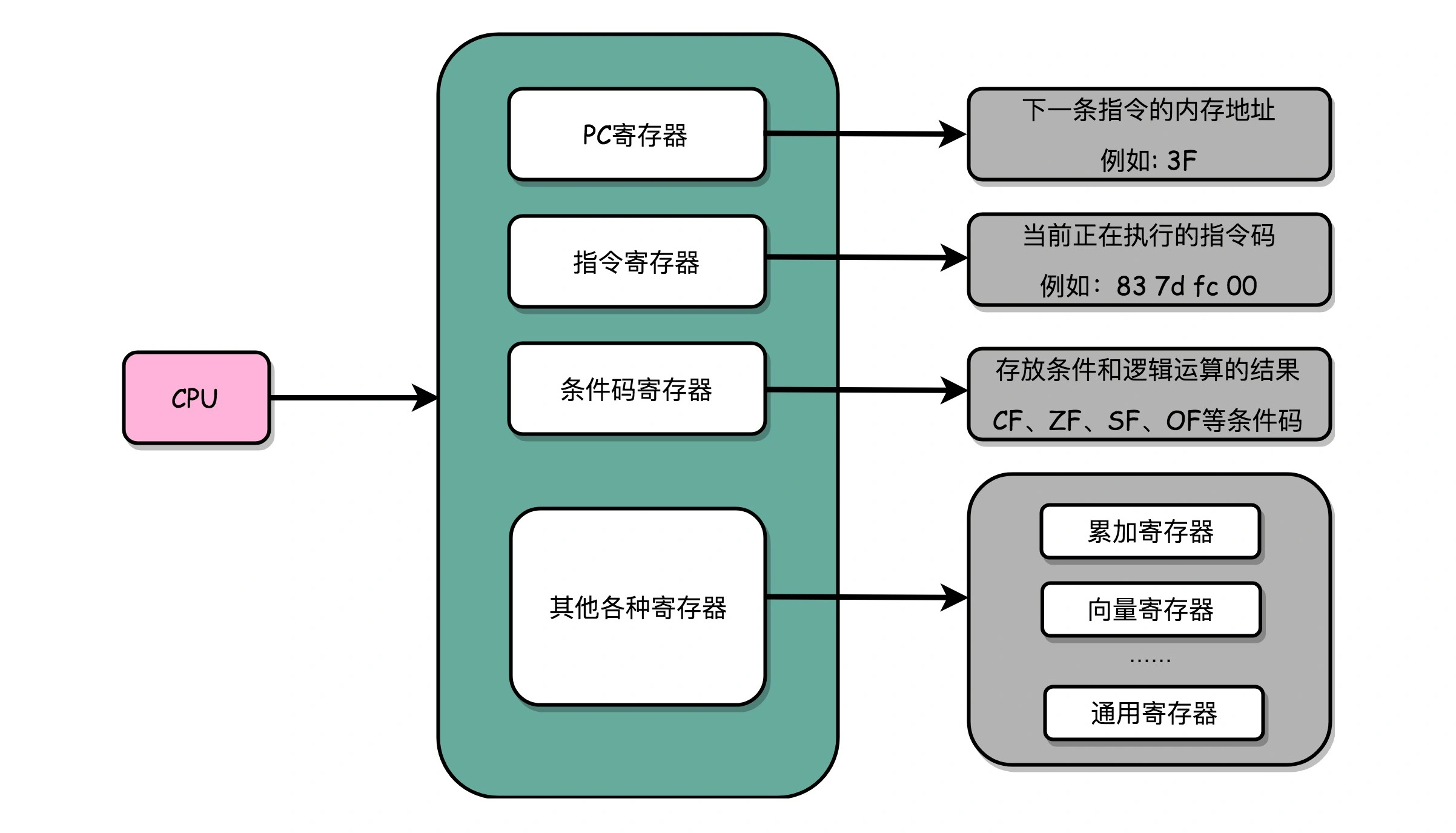
CPU中有很多不通功能的寄存器,这里有三种比较特殊的:
- PC寄存器(Program Counter Register),也叫指令地址寄存器(Instruction Address Register)。 用来存放下一条需要执行的计算机指令的内存地址。
- 指令寄存器(Instruction Register),存放当前正在执行的指令。
- 条件码寄存器(Status Register),用里面的一个一个标记位(Flag),存放CPU几星算数或逻逻辑计算的结果。
- 有些寄存器,既能存放数据,又能存放地址,我们把它叫做通用寄存器。
实际上,一个程序执行的时候,CPU会根据PC寄存器里的地址,从内存里面把需要执行的指令读取到指令寄存器里面去,然后根据指令长度自增,开始顺序读取下一条指令。可以看到,一个程序的一条条指令,在内存里面是连续保存的,并按顺序加载。
而有些特殊指令,比如上一讲我们讲到 J 类指令,也就是跳转指令,会修改 PC 寄存器里面的地址值。这样,下一条要执行的指令就不是从内存里面顺序加载的了。事实上,这些跳转指令的存在,也是我们可以在写程序的时候,使用 if…else 条件语句和 while/for 循环语句的原因。
为什么会发生stack overtflow
- 函数调用和压栈
- 函数内敛的编译器优化: 编译器自动优化的参数 -O
- 了解程序栈的概念
比较好的文章:
为什么程序无法同时在Linux和Windows下运行
格式问题
内存地址问题
- 虚拟内存
- 内存分段: 这种找出一段连续的物理内存和虚拟内存地址进行映射的方法
- 内存交换:一定程度上解决内存空间不够用的问题
- 内存分页
- 查看分页大小
$ getconf PAGE_SIZE
- 查看分页大小
动态链接、共享库
如果我们能够让同样功能的代码,在不同的程序里面,不需要各占一份内存空间,那该有多好啊!就好比,现在马路上的共享单车,我们并不需要给每个人都造一辆自行车,只要马路上有这些单车,谁需要的时候,直接通过手机扫码,都可以解锁骑行。这个思路就引入一种新的链接方法,叫作动态链接(Dynamic Link)。相应的,我们之前说的合并代码段的方法,就是静态链接(Static Link)。
在动态链接的过程中,我们想要“链接”的,不是存储在硬盘上的目标文件代码,而是加载到内存中的共享库(Shared Libraries)。顾名思义,这里的共享库重在“共享“这两个字。这个加载到内存中的共享库会被很多个程序的指令调用到。在 Windows 下,这些共享库文件就是.dll 文件,也就是 Dynamic-Link Libary(DLL,动态链接库)。在 Linux 下,这些共享库文件就是.so 文件,也就是 Shared Object(一般我们也称之为动态链接库)。
这两大操作系统下的文件名后缀,一个用了“动态链接”的意思,另一个用了“共享”的意思,正好覆盖了两方面的含义。
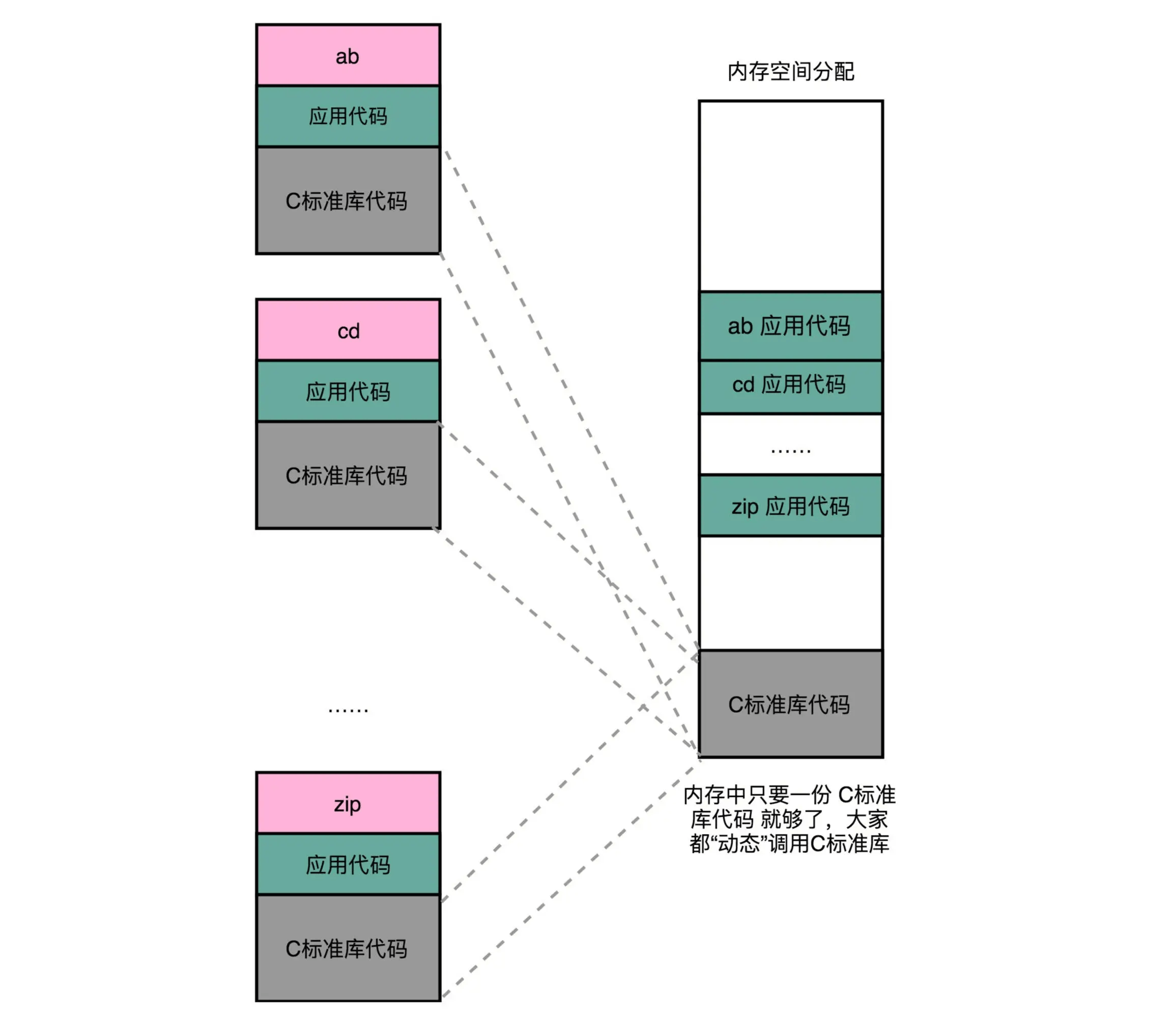
不过,要想要在程序运行的时候共享代码,也有一定的要求,就是这些机器码必须是“地址无关”的。也就是说,我们编译出来的共享库文件的指令代码,是地址无关码(Position-Independent Code)。换句话说就是,这段代码,无论加载在哪个内存地址,都能够正常执行。如果不是这样的代码,就是地址相关的代码。
动态代码库内部的变量和函数调用都很容易解决,我们只需要使用相对地址(Relative Address)就好了。各种指令中使用到的内存地址,给出的不是一个绝对的地址空间,而是一个相对于当前指令偏移量的内存地址。因为整个共享库是放在一段连续的虚拟内存地址中的,无论装载到哪一段地址,不同指令之间的相对地址都是不变的。
PLT 和 GOT,动态链接的解决方案。
参考资料
程序员的自我修养:链接、装载和库
二进制编码
如何表示负数或者为什么使用补码来表示负数:
例如二进制编码中,0011 表示为 +3 ,如果想标识一个负数,很简单的想法是用第一位表示正负,例如1表示负,0表示正。这样存在一个问题: 0会有两种字符方式 1000 和 0000,显然这是非常不合理的。 于是,想出了另外一种方式:我们仍然通过最左侧第一位的 0 和 1,来判断这个数的正负,并在计算整个二进制值的时候,在左侧最高位前面加个负号。
比如,一个 4 位的二进制补码数值 1011,转换成十进制,就是
−1×2^3 + 0×2^2 + 1×2^1 + 1×2^0比如,一个 4 位的二进制补码数值 1011,转换成十进制,就是
−1×2^3 + 0×2^2 + 1×2^1 + 1×2^0当然更重要的一点是,用补码来表示负数,使得我们的整数相加变得很容易,不需要做任何特殊处理,只是把它当成普通的二进制相加,就能得到正确的结果。

关于ASCII码:
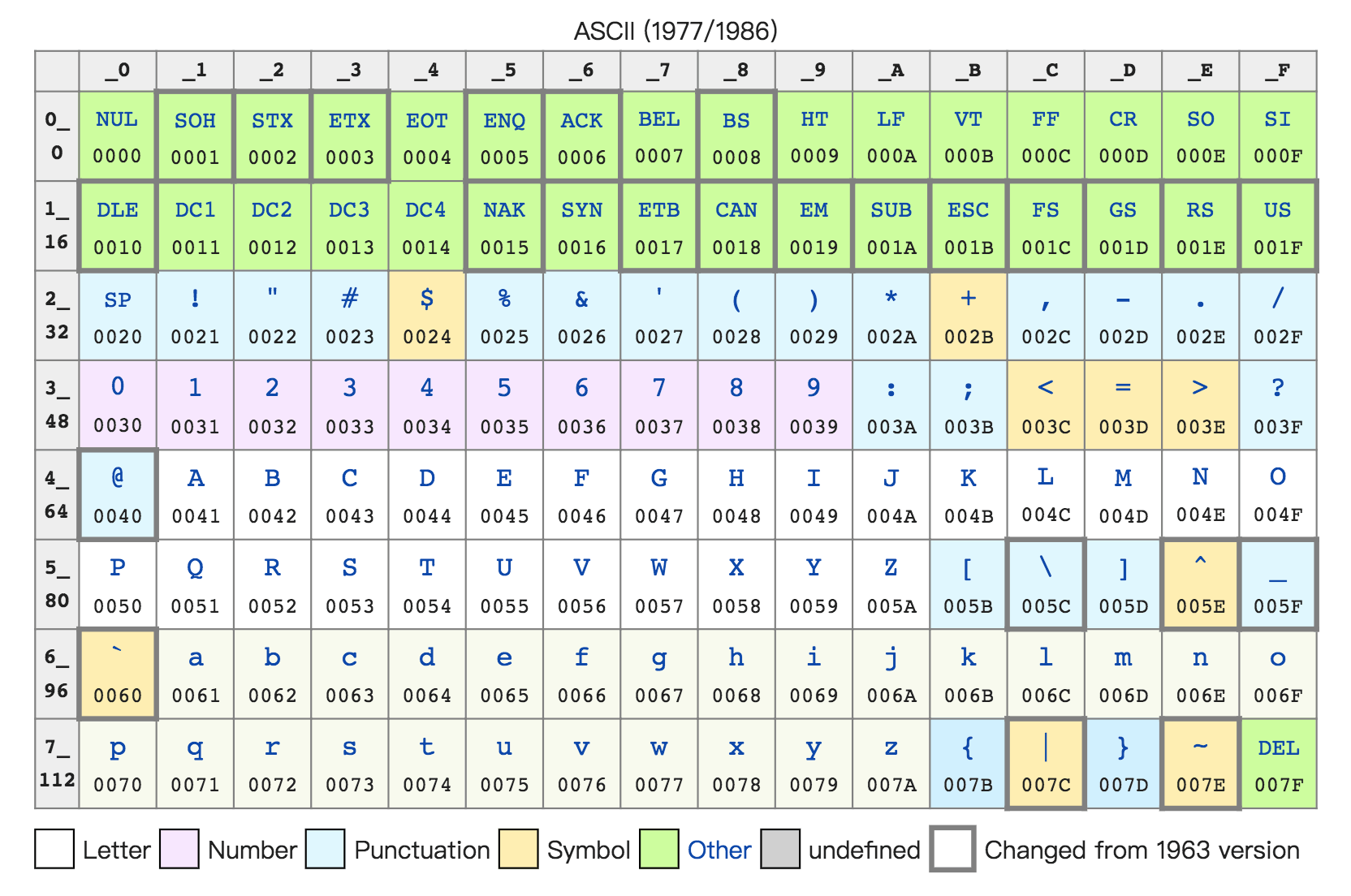
早期的时候,计算机只需要使用英文字符,加上数字和一些特殊符号,然后用 8 位的二进制,就能表示我们日常需要的所有字符了,这个就是我们常常说的 ASCII 码。
关于二进制存储更省空间的原因:
最大的 32 位整数,就是 2147483647 (2^31)。如果用整数表示法,只需要 32 位就能表示了。但是如果用字符串来表示,一共有 10 个字符,每个字符用 8 位的话,需要整整 80 位。比起整数表示法,要多占很多空间。不管是整数也好,浮点数也好,采用二进制序列化会比存储文本省下不少空间。
字符集(Charset)和字符编码(Character Encoding):
字符集顾名思义,字符的集合。我们日常说的 Unicode,其实就是一个字符集,包含了 150 种语言的 14 万个不同的字符。
而字符编码则是对于字符集里的这些字符,怎么一一用二进制表示出来的一个字典。
乱码“锟斤拷”的由来:
Unicode是一直在更新的,在这个过程中,肯定有一些比较新的字符他是无法表示的。或者即使Unicode发布了新版纳入了某个文字,但是很多软件系统并未升级也会有这样的问题。 如果匹配不到,Unicode 会统一把这些字符记录为 U+FFFD 这个编码。如果用 UTF-8 的格式存储下来,就是\xef\xbf\xbd。如果连续两个这样的字符放在一起,\xef\xbf\xbd\xef\xbf\xbd,这个时候,如果程序把这个字符,用 GB2312 的方式进行 decode,就会变成“锟斤拷”。
理解电路:从电报机到门电路,我们如何做到“千里传信”?
电报传输的信号有两种,一种是短促的点信号(dot 信号),一种是长一点的划信号(dash 信号)。我们把“点”当成“1”,把“划”当成“0”。这样一来,我们的电报信号就是另一种特殊的二进制编码了。电影里最常见的电报信号是“SOS”,这个信号表示出来就是 “点点点划划划点点点”。
- 解决长距离传输问题:继电器
如何像搭积木一样搭电路:加法
门电路:

复杂的电路可以用门电路组装起来。 例如:异或门(XOR)就是可以做最简单的整数加法(不考虑溢出进位)。
半加器理解:
- 不考虑接受低位的进位的场景
- 计算结果可以使用异或门来计算
- 是否溢出(或者说是否往高处进位)可以通过与门来计算
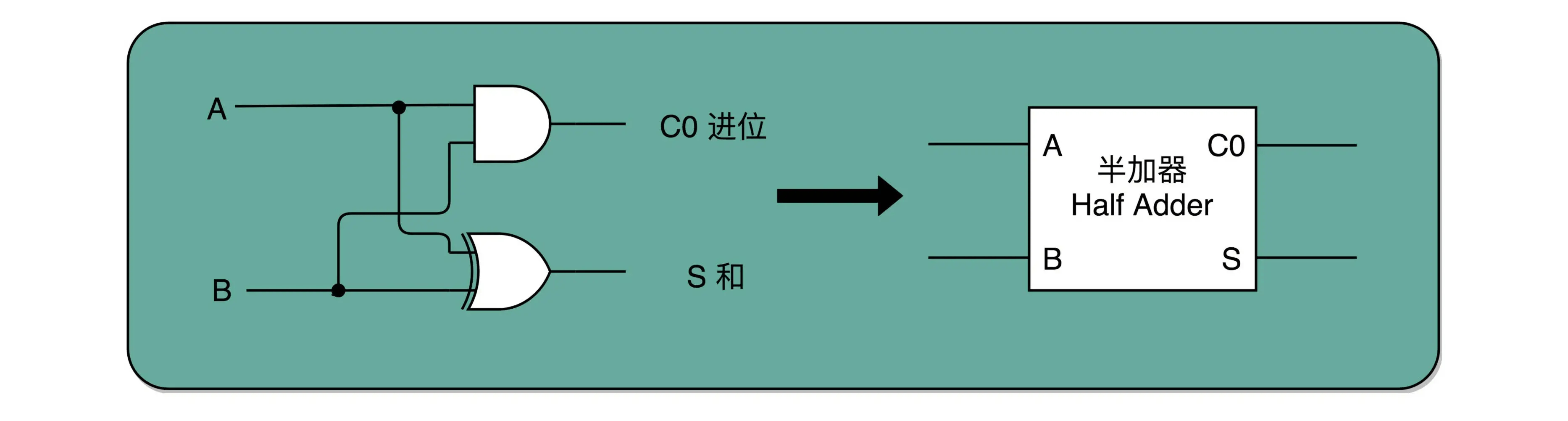
全加器:
- 和半加器的区别是需要考虑接受低位的进位
- 不会出现进两位的情况 ,例如 011 + 011 = 110
- 两个半加器和一个或门,就能组合成一个全加器
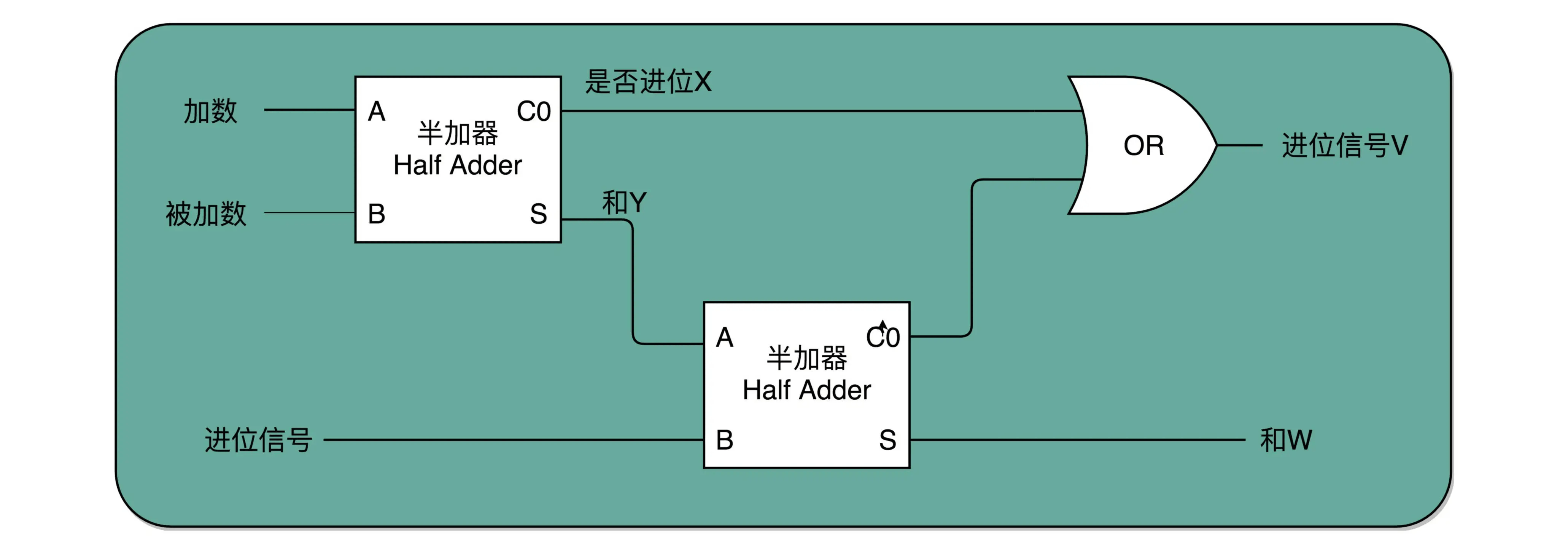
8 位加法器可以由 8 个全加器串联而成:
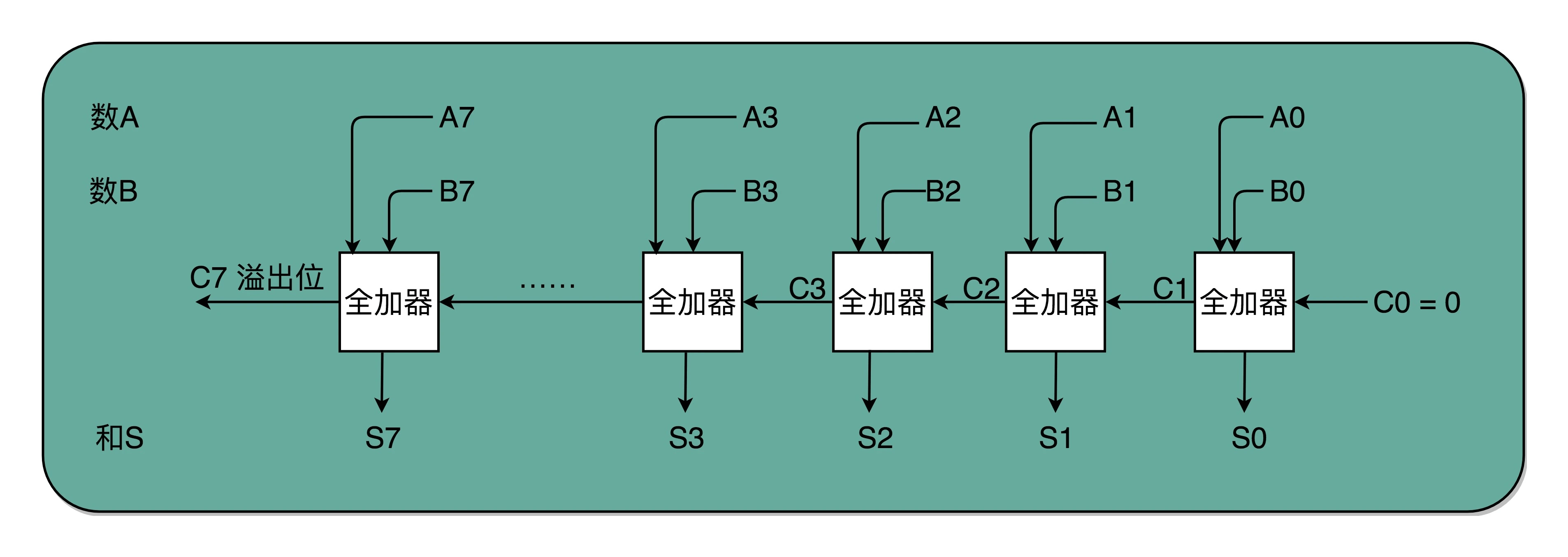
- 唯一需要注意的是,对于这个全加器,在个位,我们只需要用一个半加器,或者让全加器的进位输入始终是 0
在整个加法器的结果中,我们其实有一个电路的信号,会标识出加法的结果是否溢出。我们可以把这个对应的信号,输出给到硬件中其他标志位里,让我们的计算机知道计算的结果是否溢出。而现代计算机也正是这样做的。这就是为什么你在撰写程序的时候,能够知道你的计算结果是否溢出在硬件层面得到的支持。
如何像搭积木一样搭电路:乘法
对于乘法的实现,比较简单想法就是每一位相乘,再累加。 总结为: 位移、类加。 如图: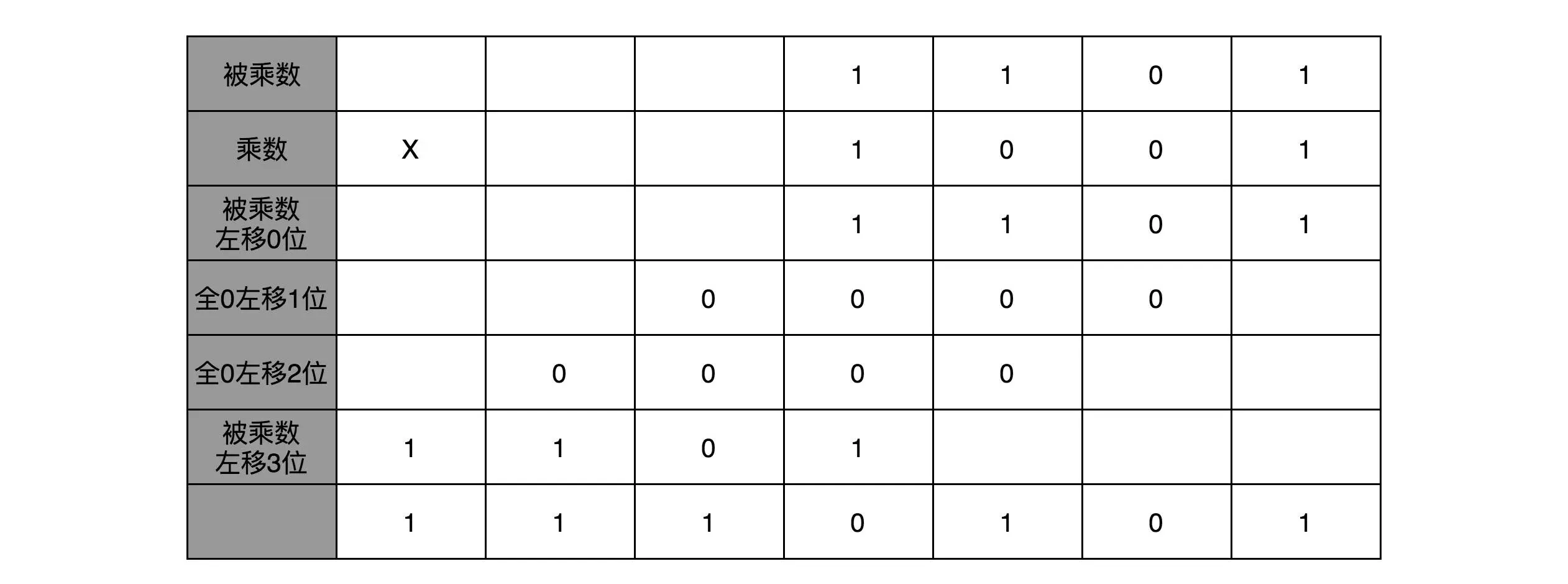
这么实现存在的问题是浪费开关,实际上,像 13×9 这样两个四位数的乘法,我们不需要把四次单位乘法的结果,用四组独立的开关单独都记录下来,然后再把这四个数加起来。因为这样做,需要很多组开关,如果我们计算一个 32 位的整数乘法,就要 32 组开关,太浪费晶体管了。如果我们顺序地来计算,只需要一组开关就好了。
我们先拿乘数最右侧的个位乘以被乘数,然后把结果写入用来存放计算结果的开关里面,然后,把被乘数左移一位,把乘数右移一位,仍然用乘数去乘以被乘数,然后把结果加到刚才的结果上。反复重复这一步骤,直到不能再左移和右移位置。这样,乘数和被乘数就像两列相向而驶的列车,仅仅需要简单的加法器、一个可以左移一位的电路和一个右移一位的电路,就能完成整个乘法。
正确性:左移一位、右移一位,可以保证乘积的大小不变(2^(-1) * 2^1 === 1)
便利性:这样每次乘法,都可以用乘数的最右一位
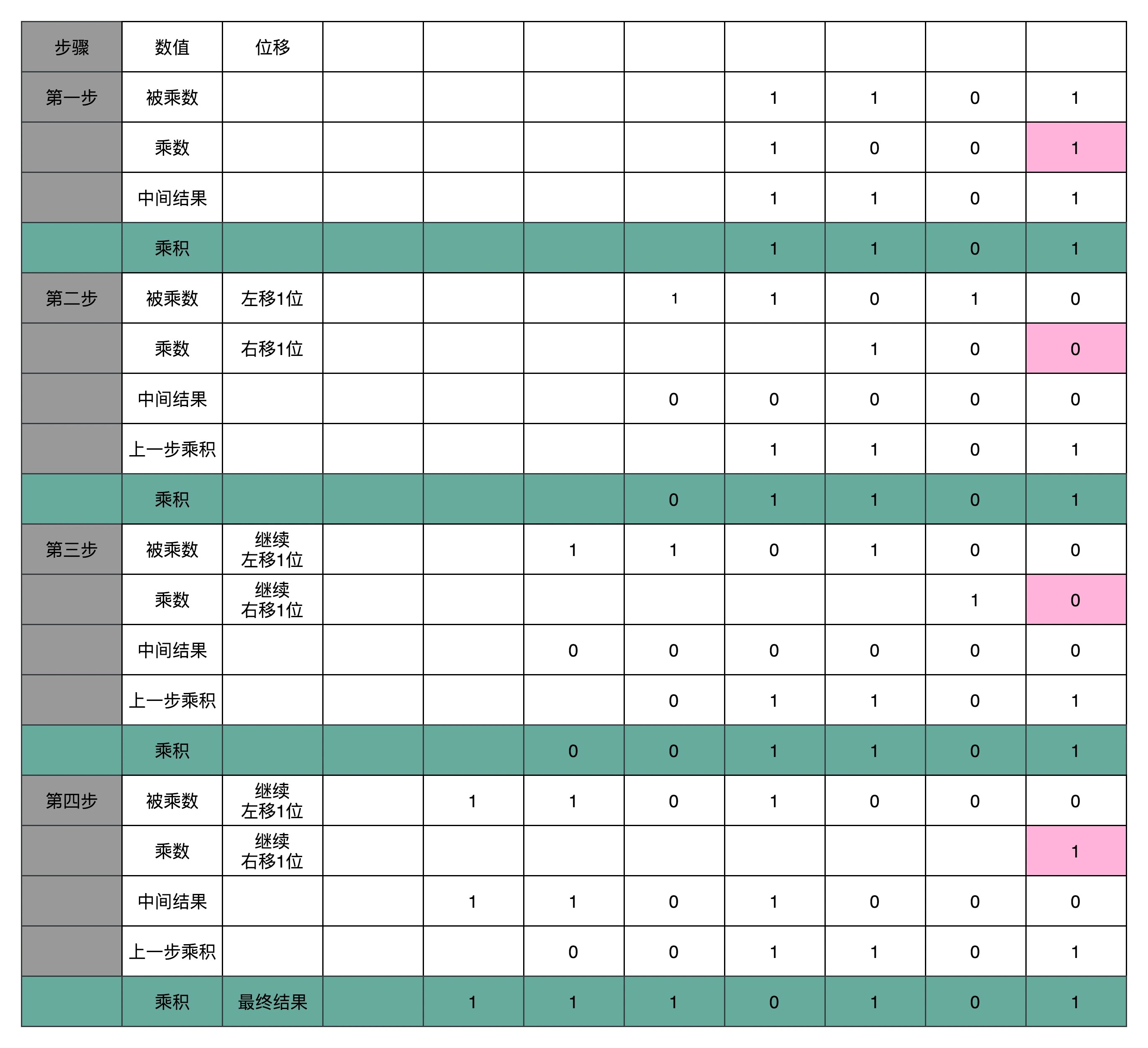
这个计算方式虽然节约电路了,但是也有一个很大的缺点,那就是慢。因为每一步的运算都依赖上一步的结果。
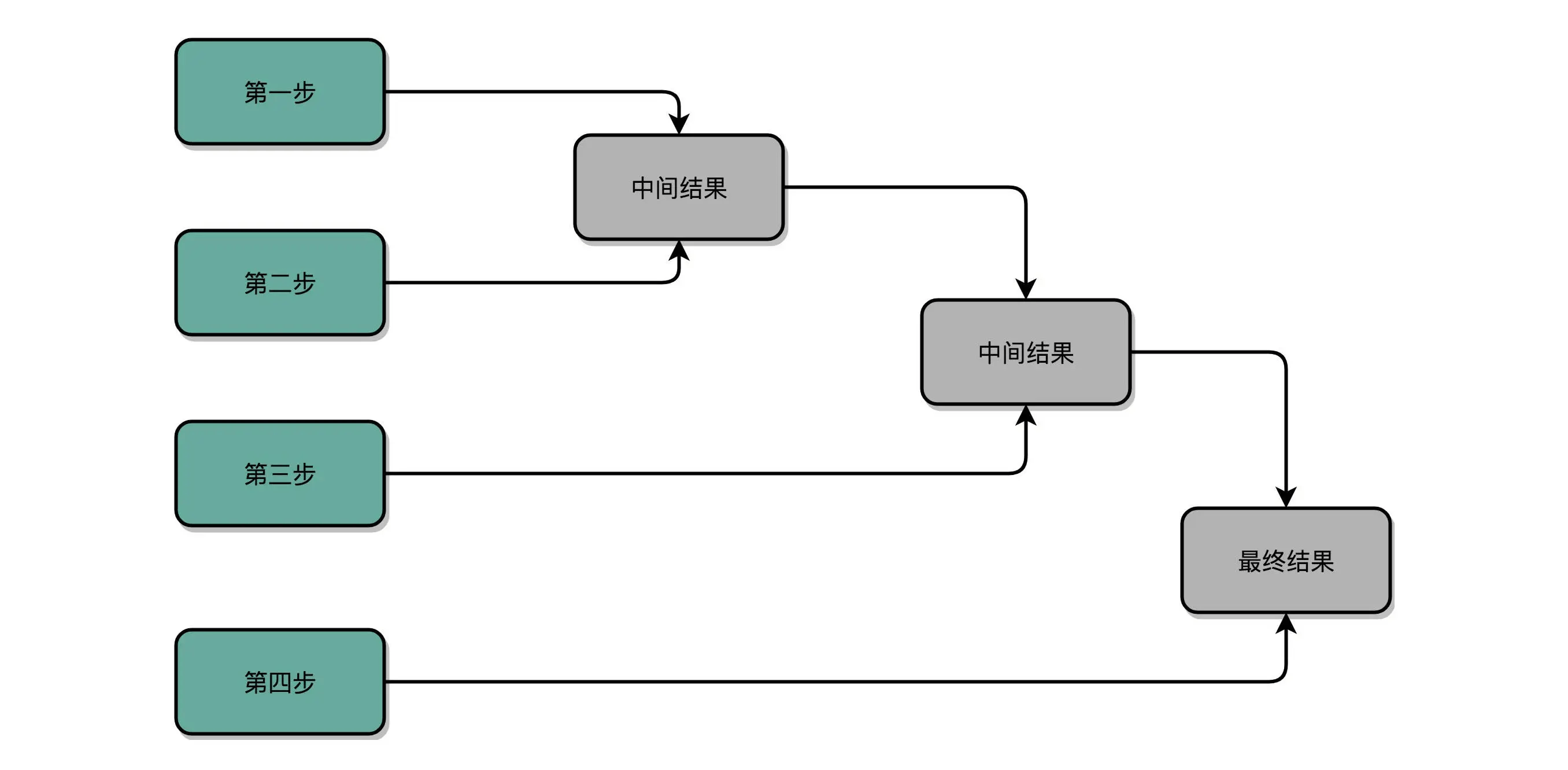
加速的办法,就是把比赛变成像世界杯足球赛那样的淘汰赛,32 个球队捉对厮杀,同时开赛。这样一天一下子就淘汰了 16 支队,也就是说,32 个数两两相加后,你可以得到 16 个结果。后面的比赛也是一样同时开赛捉对厮杀。只需要 5 天,也就是 O(log2N) 的时间,就能得到计算的结果。
但是这种方式要求我们得有 16 个球场。因为在淘汰赛的第一轮,我们需要 16 场比赛同时进行。
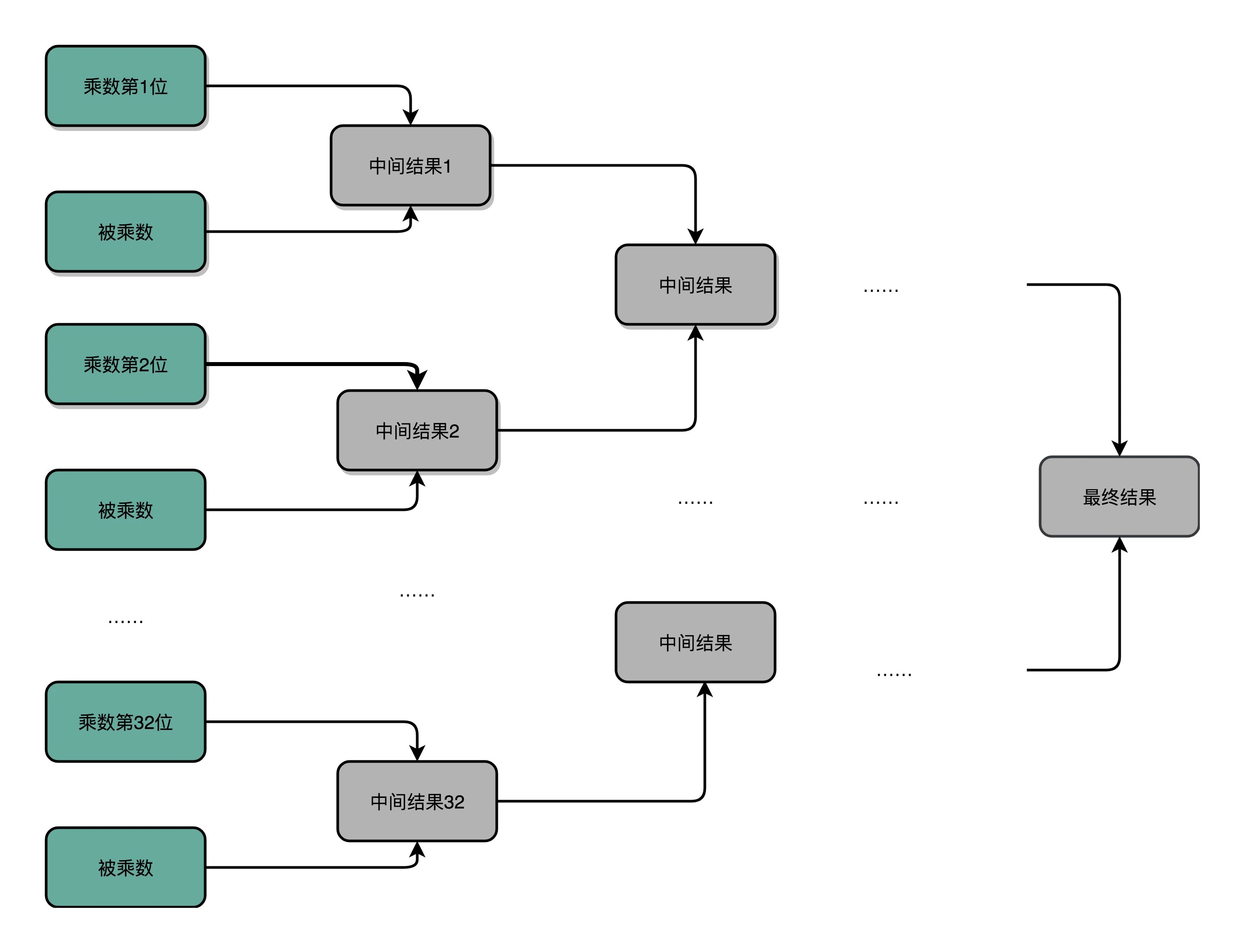
慢的问题分析:
- 门延迟(Gate Delay):每通过一个门电路,我们就要等待门电路的计算结果,就是一层的门电路延迟
- 时钟频率: 如果我们想要用更少的电路,计算的中间结果需要保存在寄存器里面,然后等待下一个时钟周期的到来,控制测试信号才能进行下一次移位和加法,这个延迟比上面的门延迟更可观。
解决方案就是:空间换时间。 如果一个 4 位整数最高位是否进位,展开门电路图,你会发现,我们只需要 3T 的延迟就可以拿到是否进位的计算结果。而对于 64 位的整数,也不会增加门延迟,只是从上往下复制这个电路,接入更多的信号而已。看到没?我们通过把电路变复杂,就解决了延迟的问题。
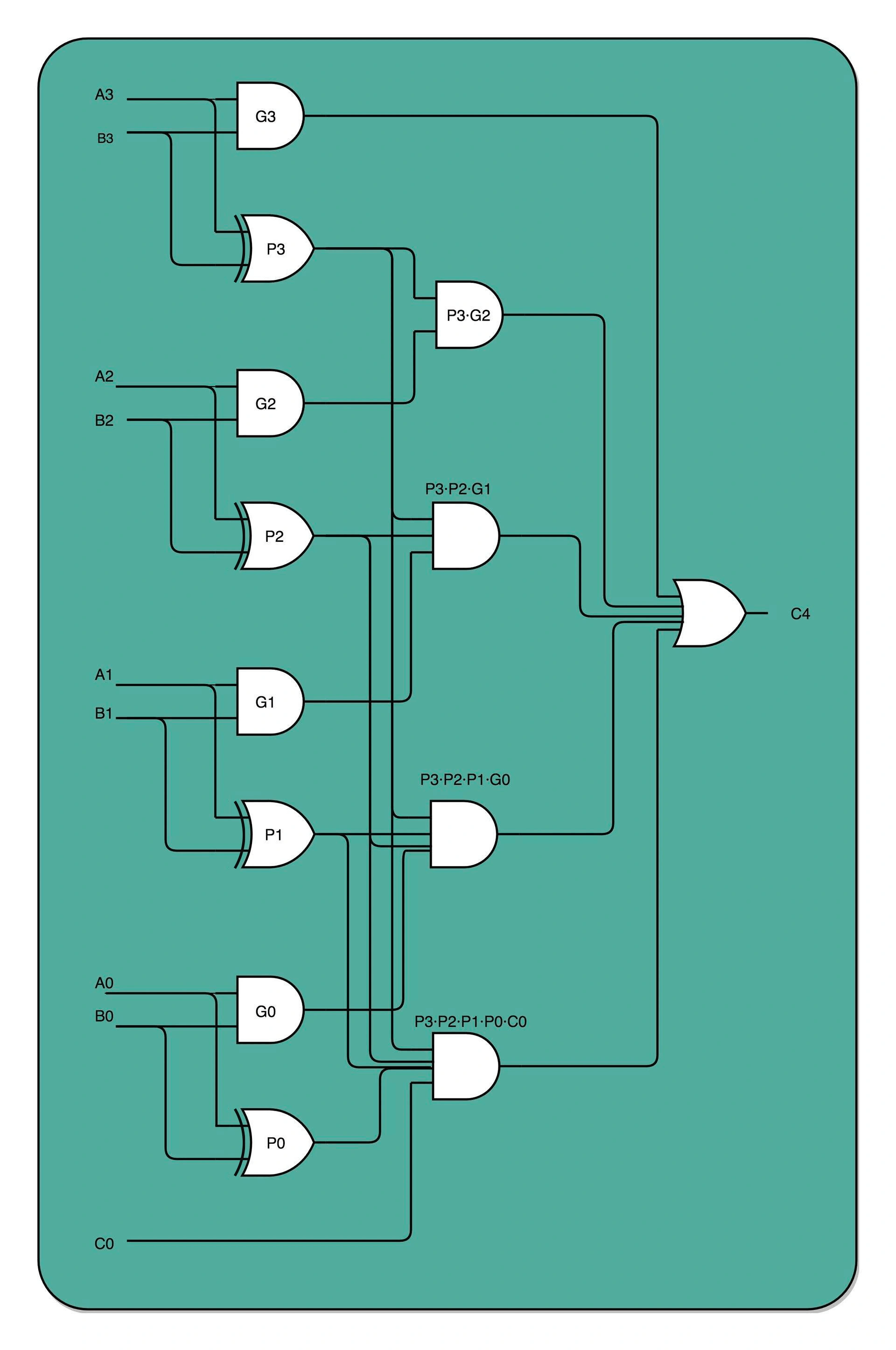
注:
这里想要解决的问题是,如果电路的“层数”太深,意味着一次运算需要的时钟循环数会太多,这样CPU就会“慢”,所以我们就把原先的电路尽量展开到比较少的层数,虽然这可能意味着电路的晶体管数量的增加。 具体到这里的加法,是把两个4位的二进制数相加,一个数A,从高位到低位是 A3A2A1A0,第二个数B,从高位到低位是 B3B2B1B0 我们加完之后的和,应该是 C4C3C2C1C0,变成5位,最高位的C4是代表这两个数相加之后是否会溢出一位需要进位。 不展开的情况下,我们计算C4,需要先算出A0和B0的和,以及是否进位,然后把是否进位,再和A1和B1相加,在看是否进位,这样一层层上来,这样的话,整个计算就需要至少5层(现在图里的是3层) 但是实际上我们可以把整个电路图展开,C4这个进位,只有这几种情况:
- A3+B3 需要进位(两个都是1)
- A3+B3是1(通过一个一个异或门)并且 A2+B2 进位。这里前面的这个就是图里第二列第一行的P3,后面是同一个节点里面的G2
- A3+B3是1,并且 A2+B2 是1,并且 A1+B1进位。对应的就是第二列第二行的 P3,P2,G1
- A3+B3是1,并且 A2+B2 是1,并且 A1+B1是1,并且A0+B0进位。对应的就是第二列第三行的 P3,P2,P1,G1
- A3+B3是1,并且 A2+B2 是1,并且 A1+B1是1,并且A0+B0是1,并且下面进位上来的标志C0是1,对应的就是第二列第四行的P3,P2,P1,P0,C0 这5个结果就是图里面的第二列的电路,都是与门。然后任意一个条件满足,C4就需要进位,所以C4是这五个 与门 并联之后的 或门。
遍历场景,将电路结构复杂,减少运算等待。
浮点数和定点数
BCD编码: 这种用二进制来表示十进制的编码方式,叫作BCD 编码(Binary-Coded Decimal)。其实它的运用非常广泛,最常用的是在超市、银行这样需要用小数记录金额的情况里。在超市里面,我们的小数最多也就到分。这样的表示方式,比较直观清楚,也满足了小数部分的计算。
- 优点
- 直观
- 计算不会存在精度问题
- 缺点
- 浪费空间
- 没办法同时表示很大的数字和很小的数字
浮点数: 
单精度的 32 个比特可以分成三部分。第一部分是一个符号位,用来表示是正数还是负数。我们一般用 s 来表示。在浮点数里,我们不像正数分符号数还是无符号数,所有的浮点数都是有符号的。接下来是一个 8 个比特组成的指数位。我们一般用 e 来表示。8 个比特能够表示的整数空间,就是 0~255。我们在这里用 1~254 映射到 -126~127 这 254 个有正有负的数上。因为我们的浮点数,不仅仅想要表示很大的数,还希望能够表示很小的数,所以指数位也会有负数。你发现没,我们没有用到 0 和 255。没错,这里的 0(也就是 8 个比特全部为 0) 和 255 (也就是 8 个比特全部为 1)另有它用,我们等一下再讲。最后,是一个 23 个比特组成的有效数位。我们用 f 来表示。综合科学计数法,我们的浮点数就可以表示成下面这样:(−1)^s × 1.f × 2^e
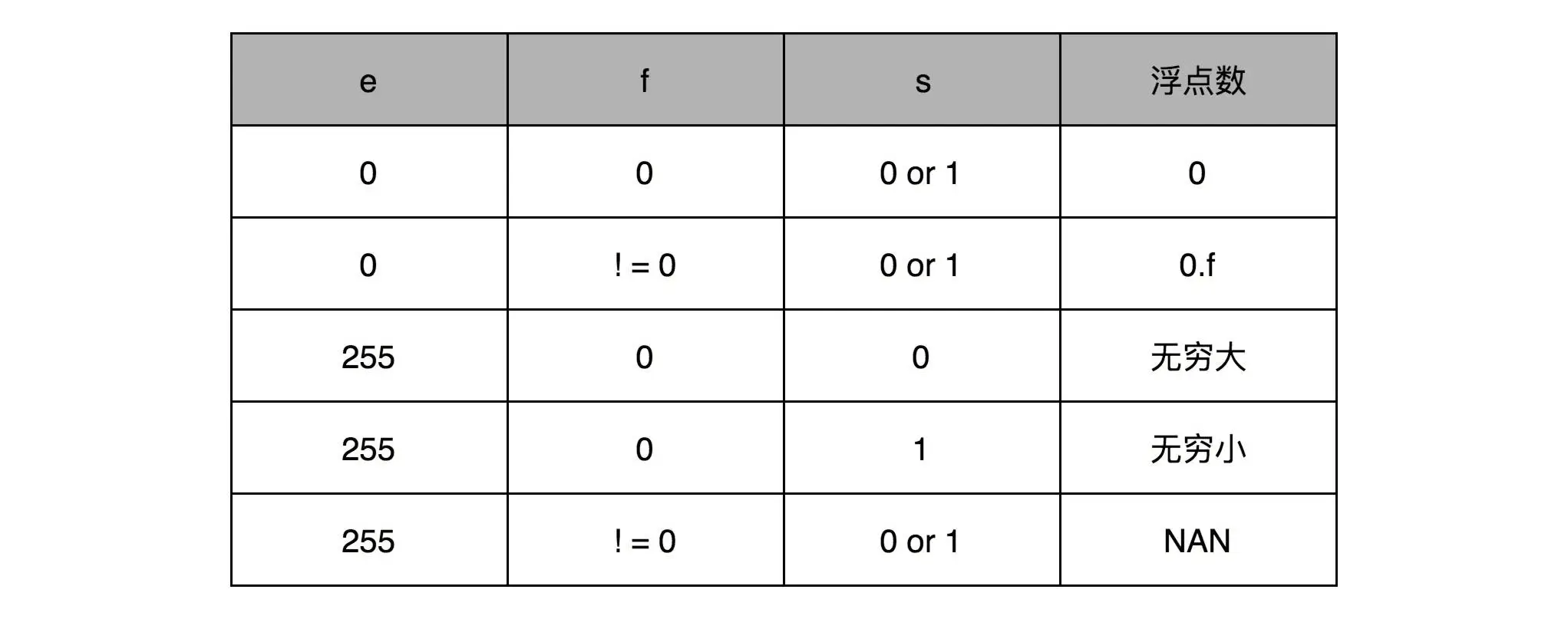
http://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html
1)(-1)^s表示符号位,当s=0,V为正数;当s=1,V为负数。
(2)M表示有效数字,大于等于1,小于2。
(3)2^E表示指数位。 (E为一个无符号整数(unsigned int)。这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,E的真实值必须再减去一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。)